二叉树的线索化

概念

二叉树的遍历是将二叉树中结点按一定规律线性化的过程。当以二叉链表作为存储结构时，仅仅能找到左右孩子信息，而不能直接得到结点在遍历序列中的前驱和后继信息。要得到这些信息有两个办法：1.将二叉树遍历一遍。在遍历过程中可得到前序和后继，2.充分利用二叉树中的空链表域。将遍历的过程中的结点的前驱和后继保存下来，实验证明另外一种方法更优。以下介绍第2种方法。

数据结构

在有n个结点的二叉树中。共同拥有2n个链表域。但仅仅有n-1个实用的非空链表域，其余n+1个都是空的，我们能够利用这n+1个链表域来存放遍历过程訪问的结点的前驱和后继。其结构例如以下图：

当中：

ltag = 0表示lchild指向结点的左孩子。ltag = 1表示lchild指向前驱；

rtag = 0表示rchild指向结点的右孩子。rtag = 1表示rchild指向后继；

在这样的存储结构中，指向前驱和后继结点的指针叫做线索，以这样的结构组成的二叉树为线索二叉树。

中序线索化

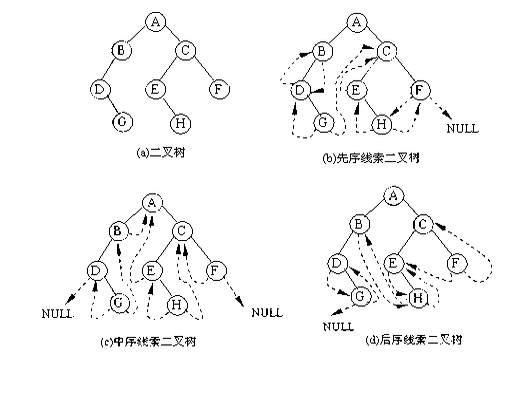
问题来了！！！为什么我们要选择中序线索化呢？例如以下图所看到的是一个二叉树的先序、中序、后序线索化过程。

二叉树的前序遍历顺序为：ABDG CEHF。假设用下划线来代表空链表域的话，则是：AB D _G C _ E _ H _ F

中序遍历顺序为:DGBAEHCF,假设用下划线来代表空链表域的话，则是：

D G _ B _ A _ E _ H _ C _ F _

后序遍历的顺序为：GDBAHEFC。假设用下划线来代表空链表域的话。则是：_ G _ D B A _ H _ _ E _ F _ C.

从先序、中序、后序线索化的过程中。能够大致看出，中序遍历的空链表域分布更均匀。在指向前驱和后继过程中更好，可是这也不是否能定前序的线索化和后序的线索化，还是依照二叉树的结构和特点以及使用场景来进行选择，在这里就仅仅说明中序线索化。

二叉树的线索化操作

二叉树的线索化操作（中序线索化）:

status InitBTree(BTree * BT)初始化建立二叉树；

void OnThread(BTree BT)二叉树线索化。

BTree FindPre(BTree BT)查找线索化结点的前驱;

BTree FindLast(BTree BT)查找线索化结点的后继；

BTree FindNode(BTree BT,char ch)查找指定结点位置；

status InsNode(BTree BT,char par,int pos, char value)线索化二叉树的插入一个结点；

BTree DelNode(BTree BT,char ch)；线索化二叉树删除一个结点。

(——————————-C语言实现———————————–)

#include "stdio.h"#include "stdlib.h"#include "string.h"#define ERROR 0#define TRUE 1typedef  int status;typedef struct BTNode{    char data;    int ltag,rtag;  //标识    struct BTNode *lchild,*rchild;}BTNode, *BTree;struct BTNode *pre = NULL;  //先前结点/*初始化二叉树，建立二叉树*/status InitBTree(BTree * BT){    //前序建立二叉树    char temp;    scanf("%c",&temp);    if(temp == '.')(*BT) = NULL;    else{        (*BT) = (BTree)malloc(sizeof(BTNode));        (*BT)->data = temp;        (*BT)->lchild = NULL;(*BT)->rchild = NULL;        (*BT)->ltag = 0;(*BT)->rtag = 0;        InitBTree(&(*BT)->lchild);        InitBTree(&(*BT)->rchild);    }    return TRUE;}//二叉树线索化void OnThread(BTree BT){    //因为二叉树的中序遍历过程中，左右孩子为空的位置分布较为均匀。所以二叉树线索化是二叉树的中序的悬索化    //二叉树的 线索化是将树形结构转化为线性结构    if(BT!=NULL){        OnThread(BT->lchild);            if(pre!= NULL && pre->rchild ==NULL){                pre->rtag = 1;                pre->rchild = BT;            }            if(BT->lchild == NULL){                if(pre !=NULL){                    BT->ltag = 1;                    BT->lchild = pre;                }            }        pre = BT;        OnThread(BT->rchild);    }}void PrintTree(BTree BT, int nLayer){ //打印二叉树竖型结构    int i = 0;    if(BT == NULL)return;    PrintTree(BT->rchild,nLayer +1);    for(i = 0; i
      
       data);    PrintTree(BT->lchild,nLayer +1);}BTree FindPre(BTree BT){  //查找结点的前驱    BTree p = NULL;    if(BT!=NULL){        if(BT->lchild ==NULL)return NULL;  //前驱结点为空        else if(BT->lchild!=NULL && BT->ltag ==1)return BT->lchild;        else if(BT->lchild != NULL && BT->ltag == 0){            p = BT;            while(p->rchild !=NULL && p->rtag !=1)p = p->rchild;            return p;        }    }    return NULL;}BTree FindLast(BTree BT){ //查找结点后继    BTree p = NULL;    if(BT!=NULL){        if(BT->rchild ==NULL)return NULL;        else if(BT->rchild !=NULL && BT->rtag ==1)return BT->rchild;        else if(BT->rchild !=NULL && BT->rtag == 0){            p = BT->rchild;            while(p->lchild != NULL && p->ltag ==0)p = p->lchild;            return p;        }    }    return NULL;}BTree FindNode(BTree BT,char ch){  //查找当前节点        BTree p = NULL;    if(BT!=NULL){        if(BT->lchild != NULL){            p = BT->lchild;            while(p->lchild !=NULL)p = p->lchild;  //找到线头        }else if(BT->lchild ==NULL){  //仅仅有右子树            p = BT;        }            while(p!=NULL){                if(p->data == ch)return p;                p = FindLast(p);        }    }    return NULL;}BTree FindParent(BTree BT,BTree p1){  //查找当前节点        BTree p = NULL;    if(BT!=NULL){        if(BT->lchild != NULL){            p = BT->lchild;            while(p->lchild !=NULL)p = p->lchild;  //找到线头        }else if(BT->lchild ==NULL){  //仅仅有右子树            p = BT;        }            while(p!=NULL){                if((p->lchild == p1 && p->ltag ==0) || (p->rchild == p1 && p->rtag ==0))return p;                p = FindLast(p);        }    }    return NULL;}status InsNode(BTree BT,char par,int pos, char value){  //par父节点data，pos代表插入的左边还是右边0代表左边，1代表右边    BTree s = NULL,last = NULL,pre1 = NULL;    BTree parent = FindNode(BT,par);    if(parent == NULL){        printf("插入位置不存在...");        return ERROR;    }    if(pos == 1){  //插入右子树        s = (BTree)malloc(sizeof(BTNode));        if(parent->rtag == 1){  //假设右子树为空            s->data = value;            s->ltag = 1;s->lchild = parent;            s->rtag = parent->rtag;            s->rchild = parent->rchild;            parent->rtag = 0;            parent->rchild = s;        }else if(parent->rtag ==0){  //右子树不为空            if(parent->rchild == NULL){                s->data = value;                parent->rchild = s;                s->rtag = 0;s->rchild = NULL;                s->ltag = 1;s->lchild = parent;                return TRUE;            }            last = FindLast(parent);  //查找到父节点直接后继            printf("后继结点:%c\n",last->data);            if(last!=NULL){                s->data = value;                s->rtag = 0; s->rchild = parent->rchild;                parent->rchild = s;                s->ltag = 1;s->lchild = parent;                last->lchild = s;            }        }    }else if(pos == 0){  //插入左子树        s = (BTree)malloc(sizeof(BTNode));        if(parent->ltag ==1){  //假设左子树为空            s->data = value;            s->ltag = parent->ltag;s->lchild = parent->lchild;            parent->ltag = 0;            s->rtag = 1; s->rchild = parent;        }else if(parent->ltag ==0){            if(parent->lchild == NULL){                s->data = value;                parent->lchild = s;                s->ltag = 0;s->lchild = NULL;                s->rtag = 1;s->rchild = parent;                return TRUE;            }            pre1 = FindPre(parent);            s->data = value;            s->ltag = parent->ltag;            s->lchild = parent->lchild;            parent->lchild = s;            s->rtag = 1;            s->rchild = parent;            pre1->rchild = s;        }    }    return TRUE;}BTree DelNode(BTree BT,char ch){  //删除结点    BTree parent = NULL,p = NULL,temp = NULL,temp1 = NULL;    p = FindNode(BT,ch);    if(p == NULL){        printf("二叉树无此结点\n");        return ERROR;    }    parent = FindParent(BT,p);    if(parent == NULL){ //删除根结点，顶点        temp = FindPre(p);  //找到根节点的先驱        temp->rtag = 0;temp->rchild = p->rchild;        if(p->rchild->ltag == 1)p->lchild = temp;        temp1 = BT->lchild;        free(BT);        return temp1;    }else if(p->ltag == 1 && p->rtag == 1){        if(parent->lchild == p){            parent->ltag = p->ltag;            parent->lchild = p->lchild;        }else if(parent->rchild == p){            parent->rtag = p->rtag;            parent->rchild = p->rchild;        }        return BT;    }else if(p->ltag  == 0 && p->rtag ==0){  //有左右子树        if(parent->rchild == p){            temp = FindPre(p);            parent->rchild = p->lchild;            temp->rtag = 0;temp->rchild = p->rchild;            free(p);        }else if(parent->lchild == p){            temp = FindLast(p);            parent->lchild = p->rchild;            temp->ltag = 0;temp->lchild = p->lchild;            free(p);        }    }    return BT;}void OnOrder(BTree BT){ //遍历    BTree p = NULL;    printf("线索化的遍历:\n");    if(BT!=NULL){        if(BT->lchild != NULL){            p = BT;            while(p->lchild !=NULL && p->ltag ==0)p = p->lchild;  //找到线头        }else if(BT->lchild ==NULL){  //仅仅有右子树            p = BT;        }            while(p!=NULL){                printf("%c",p->data);                p = FindLast(p);        }    }    printf("\n");}/*主函数*/void main(){    BTree BT = NULL;  //初始化    BTree temp1 = NULL;    char input;    printf("请输入前序二叉树,空结点以.表示:\n");    InitBTree(&BT);  //建立二叉树    getchar();    printf("打印二叉树的树形结构:\n");    PrintTree(BT,1);  //    OnThread(BT); //线索化二叉树    OnOrder(BT);  //依据线索遍历    //查找某一节点    printf("请输入要查找的字符:");    scanf("%c",&input);    getchar();    temp1 = FindNode(BT,input);    if(temp1 ==NULL)printf("查找失败...\n");    else printf("查找到%c\n",temp1->data);    InsNode(BT,'B',0,'K');    printf("插入后遍历:\n");    OnOrder(BT);  //依据线索遍历}